Research archiv
Quantum Measurements
The measurement process lies at the heart of quantum physics due to the fundamentally probabilistic measurement outcome and the projection of the wavefunction onto an eigenspace of the measurement observable. The instantaneous backaction of a measurement device on the system under test also leads to fundamental bounds on the accuracy with which one can gain information about a system with minimal disturbance. Quantum Measurements are also of great importance for performing error syndrome detection in error-correcting codes. Our research aims at advancing today’s quantum measurement capabilities, e.g. by developing quantum-limited amplifiers [1,2], photon detectors [3], and measurement apparatus to readout qubits with high fidelity, speed, bandwidth, and resource-efficiency [4,5].
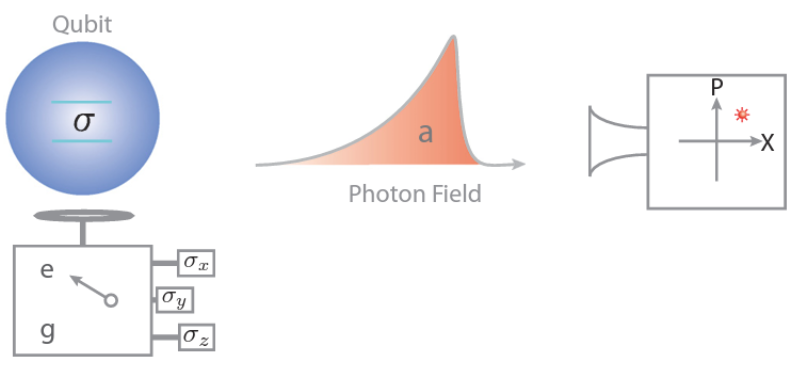
Schematic representation of a measurement apparatus performing qubit readout (left) and amplitude detection of a propagating radiation field (right).
References
- [1] Controlling the dynamic range of a Josephson parametric amplifier, C. Eichler, and A. Wallraff, EPJ Quantum Technology 1, 2 (2014).
- [2] Quantum-Limited Amplification and Entanglement in Coupled Nonlinear Resonators, C. Eichler, Y. Salathe, J. Mlynek, S. Schmidt, and A. Wallraff, Phys. Rev. Lett. 113, 110502 (2014).
- [3] Single-Shot Quantum Non-Demolition Detection of Individual Itinerant Microwave Photons, J. – C. Besse, S. Gasparinetti, M. C. Collodo, T. Walter, P. Kurpiers, M. Pechal, C. Eichler, and A. Wallraff, Phys. Rev. X 8, 021003 (2018).
- [4] Rapid, High-Fidelity, Single-Shot Dispersive Readout of Superconducting Qubits, T. Walter, P. Kurpiers, S. Gasparinetti, P. Magnard, A. Potoćnik, Y. Salathe, M. Pechal, M. Mondal, M. Oppliger, C. Eichler, and A. Wallraff, Phys. Rev. Appl. 7, 054020 (2017).
- [5] Rapid High-fidelity Multiplexed Readout of Superconducting Qubits, J. Heinsoo, C. Kraglund Andersen, A. Remm, S. Krinner, T. Walter, Y. Salathe, S. Gasparinetti, J-C. Besse, A. Potocnik, A. Wallraff, and C. Eichler, Phys. Rev. Appl. 10, 034040 (2018).
Hardware for Error-Corrected Quantum Computing
Quantum Computers will ultimately rely on near-perfect logical gates, implemented while correcting errors at the physical level. The need for developing quantum hardware optimized for performing fast, repeatable, and high-fidelity syndrome measurements in quantum error-correcting codes such as the surface code therefore becomes increasingly important. Based our advances in performing qubit readout and two-qubit gates in multi-qubit superconducting quantum processors, we could recently demonstrate repeated quantum error correction in a surfaces code. Our research aims at developing superconducting quantum hardware to enhance the speed and fidelity of syndrome detection and study elements of universal quantum computing with logically encoded qubits.
References
- [1] Realizing repeated quantum error correction in a distance-three surface code. Sebastian Krinner, Nathan Lacroix, Ants Remm, Agustin Di Paolo, Elie Genois, Catherine Leroux, Christoph Hellings, Stefania Lazar, Francois Swiadek, Johannes Herrmann, Graham J. Norris, Christian Kraglund Andersen, Markus Müller, Alexandre Blais, Christopher Eichler, and Andreas Wallraff. Nature 605.7911 (May 2022), pp. 669–674.
- [2] Entanglement stabilization using ancilla-based parity detection and real-time feedback in superconducting circuits. Christian Kraglund Andersen, Ants Remm, Stefania Lazar, Sebastian Krinner, Johannes Heinsoo, Jean-Claude Besse, Mihai Gabureac, Andreas Wallraff, and Christopher Eichler. npj Quantum Information 5 (Aug. 2019), p. 69. arXiv: 1902.06946 [quant-ph].
- [3] Repeated Quantum Error Detection in a Surface Code. Christian Kraglund Andersen, Ants Remm, Stefania Lazar, Sebastian Krinner, Nathan Lacroix, Graham J. Norris, Mihai Gabureac, Christopher Eichler, and Andreas Wallraff. Nature Physics 16 (June 2020), pp. 875–880.
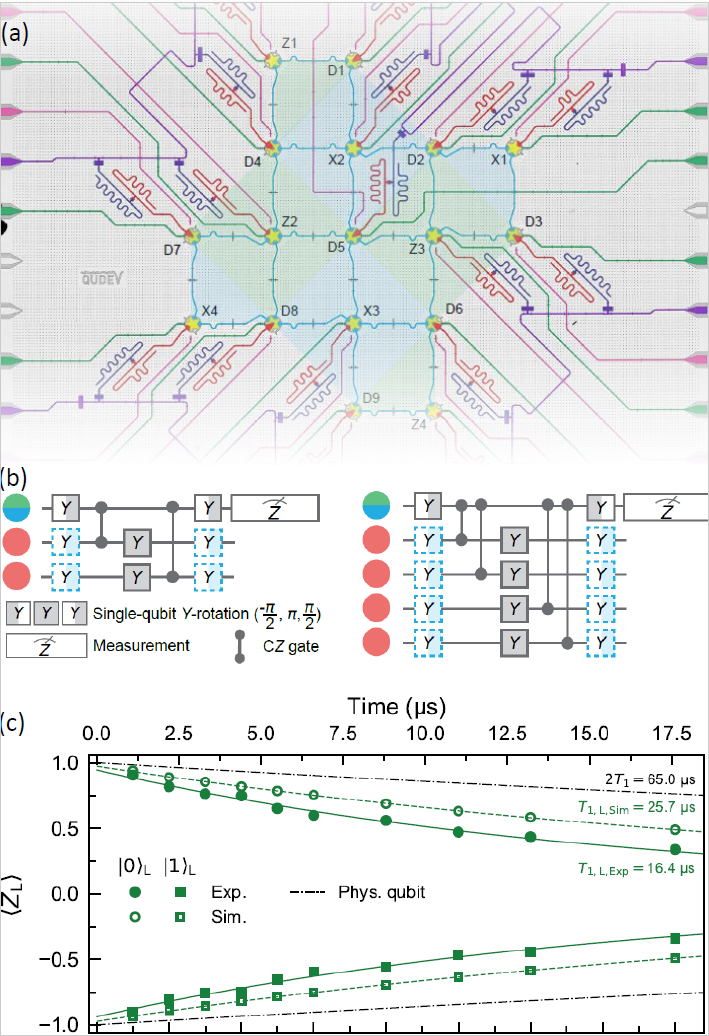
Image of the 17-qubit quantum processor used for the experiments in Ref. [1] a), quantum circuits of stabilizer measurements (b), and logical lifetime measurement in (c). See Ref. [1] for details.
Optical Simulation and Design
Optical systems consist nowadays of many different optical elements like lenses, aspheric surfaces, and mirrors, but also waveguides, diffractive optical elements, etc. Although all these elements can in principle be described by Maxwell’s equations, a practical simulation of optical systems requires many different approximate methods and their combination, since a direct solution of Maxwell’s equations is only possible analytically for a few simple cases or numerically for quite small elements.
Therefore, the research in the group of Norbert Lindlein mainly focuses on the simulation and also the design of optical systems by using for example ray tracing for aberration calculations and incoherent illumination systems, wave-optical scalar simulation methods for calculating diffraction problems or waveguides, or a vectorial formulation of the Debye integral for calculating the electromagnetic field in the vicinity of the focal region including polarization effects. In most cases, the combination of several of these methods enables a quite efficient and sufficiently accurate simulation of complex optical systems.
References
- A new 4p-geometry optimized for focussing onto an atom with a dipole-like radiation pattern. N. Lindlein, R. Maiwald, H. Konermann, M. Sondermann, U. Peschel, G. Leuchs. Laser Physics 17(7) (2007) 927-934.
- Flexible beam shaping system using Fly’s eye condenser. N. Lindlein, A. Bich, M. Eisner, I. Harder, M. Lano, R. Voelkel, K. Weible, M. Zimmermann. Appl. Opt. 49(12) (2010) 2382-2390.
- Telecentric line scanning system based on a ring surface mirror for inline processes. F. Loosen, N. Lindlein, K. Donner. Advanced Optical Technologies 5(3) (2016) 259-264.
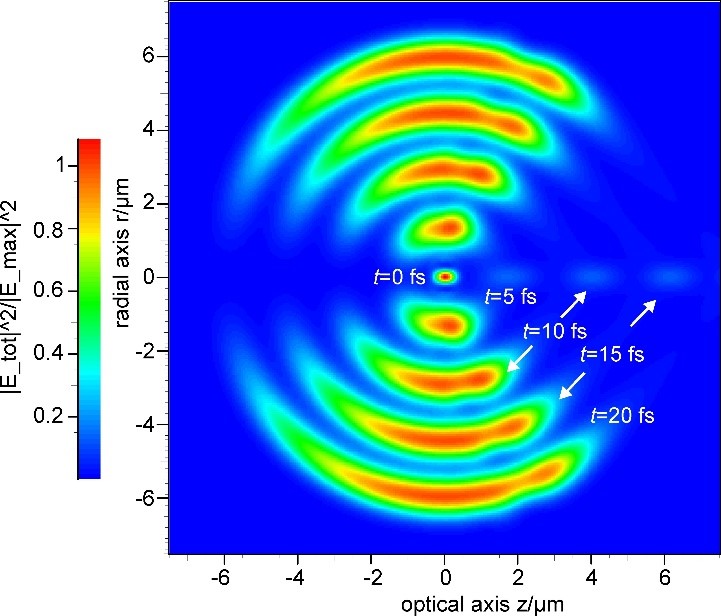
Normalized electric energy density in the focal region of a deep parabolic mirror where in total an incident ultrashort dipole wave pulse with radial polarization is generated. The simulation shows the pulse propagation at different times from t=0 fs to t=20 fs and normalized for each time separately, where t=0 is the time where the pulse maximum reaches the focal point.